Research Article - European Journal of Applied Engineering and Scientific Research ( 2018) Volume 6, Issue 2
This study was undertaken to study the graphitization tendency with optimized properties for thin wall grey iron (TWGI) and predict the hardness and tensile properties by applying multivariate regression analysis. 0.3wt % addition of Ferrosilicon (FeSi) was used for the inoculation of different wall thickness of 2, 3, 4, 5, 6, 7, 8, 9 and 10 mm of the Grey Iron. The inoculation was done in the ladle and the different wall thickness was analyzed. The result reveals carbide and pearlite formation at the lower thickness. Graphitization and flakes distribution in the cast was evident from 6 mm wall thickness. Hardness and strength results also reveal the rapid disappearance of the carbide in ferrite microstructure of the thinner walls. Stability was found in the hardness properties analyzed at the point of graphite formation and flake distribution of the less thin walls. Regression analysis was carried out using the Origin Lab Pro software and MS Excel on the data obtained from the hardness and strength test. The prediction model for the thin wall properties were obtained using convergence multivariate regression analysis (heuristic method) through the generalized reduced gradient (GRG) function. The GRG function was employed to obtain the least sum of squares deviation using the prediction model. The model is used to predict the intermediate hardness/strength value between the experimented and non-experimented wall thickness which this research could not accommodate.
Thin-wall, Graphitization, Microstructure, Inoculation, Modeling, Multivariate Regression
The development of thin wall grey iron (TWGI) is essential to designers for components which can compete favorably with aluminum for energy and fuel economy especially in higher strength temperature service application. In order to achieve fuel economy in automotive industry, reducing the vehicle weight has been a major research area of interest over the last few decades. The comparison between aluminium and grey iron is encouraged by the increased strength, ductility, stiffness, vibration damping capacity, as well as reduced cost offered by the latter according to Dix et al. [1]. When mechanical properties, density, service temperature and cost are included in material evaluation, grey iron may offer more advantages than aluminium, particularly if thin wall grey iron parts could be produced without further heat treatment processes or less expensive heat treatment process based on Showman and Aufderheide’s work [2].
The potentials for grey iron applications for lightweight automotive components have been limited by the capability to produce as-cast carbide free thin wall parts (2-3 mm). Study reveals that thin-wall grey iron has been successfully produced for many years, with the optimization of some critical production parameters: pouring temperature, chemical composition, thermal conductivity of the moulding materials, type and amount of inoculating material in combination with the casting design and other basic foundry practices as reported by Dix et al. [1].
Walled castings are prone to chilling effects. This effect is undesirable on the casting products for engineering applications. Thin wall castings undergo rapid solidification which precipitates cementite instead of flake graphite and this effect can be annulled by addition of appropriate inoculants based on Fras et al.’s work [3]. The first metal to solidify in hypoeutectic grey iron is primary austenite. As cooling continues, the remaining iron grows richer in dissolved carbon. Eventually, this liquid reaches the eutectic composition of 4.3% carbon equivalent, at which final or eutectic solidification starts under equilibrium condition according to Elkem [4]. However, equilibrium solidification does not occur under the practical foundry conditions. Due to variations in chemistry, pouring temperature, solidification rate, section thickness and other conditions, the metal will cool below the eutectic temperature before the start of final solidification as reported by Cuttino [5]. This research helps to study the mechanical properties of varying grey iron walls and predict possible hardness and strength properties at different wall thickness using a (GRG) multivariate regression model.
Material used for the research include: foundry sand, bentonite, engine block and cast iron scraps and ferrosilicon. Moulding boxes, rod-sample pattern, weighing balance, spike rod and crucible pit furnace were employed as tools and equipment.
The test pattern, mould and gating system were designed as shown in Figures 1 and 2.
Figure 1: 2D schematics of the gating system.
Figure 2: 2D schematics of the mould.
The casting has a plate shape with dimensions of 80 mm × 60 mm and 2, 3, 4, 5, 6, 7, 8, 9 and 10 mm thickness. The moulds were made of sodium silicate bonded sand. The pouring time is given by the function below according to Showman and Aufderheide [2].
For mass less than 450 kg
[Pouring time T=k ((1.41) + (T/14.59))√W]
Where K=fluidity of iron in inches/40, T=average section thickness, W= mass of the casting kg.
For mass greater than 450 kg
[Pouring time T=k ((1.236) + (T/16.65))√W]
Relevant charge calculation was carried out and in-mould inoculation was used for ferrosilicon addition. Varying thickness of grey cast iron plate was produced and finishing operation was carried out. The samples were then subjected to hardness testing using the RST3 hardness testing machine (complaint with ASTM C1624). Tensile strenght of the varying plates were analysed using the 600-SS Hydraulic Universal Test Machine according to the ASTM A48 Class 20. Microstructural examination was carried out using olympus GX-41 in line with ASTM A247.
Regression analysis is used for the study of relationships between one or several predictors and the response according to Fisher [6]. Using the MS Excel graphical analysis platform, the best fit parameters were of the hardness and strength data were obtained. This was used to route the regression model according to the linear function:
y=A0+A1 x1+A2x2+…Akxk+ϵ
Where A0, B1, B2, Bk are coefficient and ϵ is the random error [7].
The chemical compositions obtained from spectrometric analysis of charged scrap, un-inoculated sample and the inoculated sample of fixed composition of 0.3 wt% inoculants are shown in Tables 1 and 2.
| %Si | %C | %Mn | %P | %S | %Cr | %Ni | %Mo | %Cu | %Al | %Mg | %Fe |
| 1.94 | 3.97 | 0.87 | 0.088 | 0.131 | 0.163 | 0.058 | 0.0015 | 0.137 | 0.0058 | 0.0033 | 92.5 |
Table 1: Major elemental composition of used scrap
| Element | C | Si | Mn | P | S | Cr | Ni | Mo | CE |
|---|---|---|---|---|---|---|---|---|---|
| Un-inoculated Sample | 3.04 | 2.09 | 0.38 | 0.10 | 0.12 | 0.15 | 0.03 | 0.03 | 3.77 |
| Inoculated Sample 0.3 wt% | 2.97 | 2.41 | 0.37 | 0.07 | 0.18 | 0.08 | 0.05 | 0.008 | 3.797 |
Table 2: Chemical composition of un-inoculated sample (Control) and Inoculated sample (0.3% wt.)
Carbon Equivalent (CE)=TC%+1/3 [Si%+P%]
The Carbon Equivalent (CE) for 0% ferro-silicon=3.04%+1/3 [2.09%+0.100%]=3.77%
Carbon Equivalent (CE)=TC%+1/3 [Si%+P%]
The Carbon Equivalent (CE) for 0.3% ferro-silicon=2.97%+1/3 [2.41%+0.071%]=3.797%
Microstructure
The graphite morphologies of the inoculated irons (0.3wt% inoculants) for the samples of thickness from 2-10 mm, respectively are shown in Figures 3-11.
Figures 3-5 shows characterised with non-presence of carbon as graphite but as carbide with Pearlitic and Phosphorus Eutectic (shown by the marked line.
.
Figure 3: 2 mm wall thickness.
Figure 4: 3 mm wall thickness.
Figure 5: 4 mm wall thickness.
Figures 6-8 show the gradual presence of carbon as graphite with pearlitic-ferritic matrix without the phosphorus eutectic.
Figure 6:5 mm wall thickness.
Figure 7:6 mm wall thickness.
Figure 8:7 mm wall thickness.
Figures 9-11 shows reveals flake graphite type C (Kish Graphite) with increased presence of graphite network.
Figure 9:8 mm wall thickness.
Figure 10:9 mm wall thickness.
Figure 11:10 mm wall thickness.
The microstructures reveal the carbide/graphite distribution in the TWGI with the addition of 0.3wt % inoculant and also the effectiveness of the inoculant in its additions and practice. Graphite formation is not imminent with thickness of 2-5 mm due to rapid solidification as a result of wall thickness; an indication of the presence of cementite present in the iron as reported by Fotheringham and Wong [7]. It is clear that the 2 mm thickness contains considerable amount of carbides while at 5 mm, there are only traces. Between 6-10 mm wall thicknesses, solidification is rather slow and this allows graphitization and coarse pearlite formation. Increase in thickness of cast product, brings about increase in formation of graphite flakes and its distribution based on [8].
The characterization of the un-inoculated sample as shown in Table 2 reveals that there is a higher tendency of carbide formation in the cast. This is prevalent in the light of high carbon and lower silicon content. Increased carbon in the cast therefore implies the decrease or non-presence of graphite flakes in the un-inoculated cast which is best described as white cast iron [9]. Characterization result of the inoculated sample in Table 2 reveals the tendency for the presence of graphite flakes. The incidence of the high silicon content and low carbon content would amount to a greater degree of decomposition of the cementite and more coarse graphite flakes. This is because silicon increases the instability of cementite, producing graphite instead of cementite also reported by Zhou [10]. Graphite and pearlite distribution is observed from the microstructure in 5 mm wall thickness which is noticed to increase with the wall thickness as more graphite flakes is formed in the free ferrite matrix. Increasing wall thickness features more stable pearlite and pronounced graphite morphology.
Effect of inoculation on hardness properties
The hardness values vary with the section thickness as recorded. It was found that the 2 mm thickness has greatest hardness value and it decreases with increased thickness with 10 mm as the lowest. The thicker sections (6-10 mm), which was slowly cooled, are graphitic and consequently softer [11]. The reduction in the carbide content which brings about a decrease in the hardness lowers the brittleness of the grey cast iron which is also noted by Fisher [6] and Chisamera et al. [12].
Mechanical test results
The hardness and tensile strength results of sample with varying thickness were recorded with the unit of the hardness is HRA and MPa, respectively. The results are as follows in Table 3.
| Thickness values (mm) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Control X |
|---|---|---|---|---|---|---|---|---|---|---|
| Hardness 1 | 67.4 | 62.8 | 58.1 | 56.4 | 55.7 | 51.9 | 53.4 | 50.7 | 50.5 | 52.9 |
| Hardness 2 | 68.1 | 66.2 | 60.1 | 56.5 | 52.9 | 52.1 | 51.4 | 50.8 | 50.1 | 53.2 |
| Hardness 3 | 70.0 | 66.9 | 58.5 | 53.3 | 54.6 | 53.5 | 52.1 | 50.3 | 50.3 | 53.6 |
| Average value of HRA | 68.5 | 65.3 | 58.9 | 55.4 | 54.4 | 52.5 | 52.3 | 50.6 | 50.3 | 53.23 |
| Average Tensile Strength (MPa) | 1137 | 965 | 731 | 627 | 596 | 573 | 569 | 537 | 524 | 571 |
Table 3: Experimental Rockwell hardness and tensile strength test results of grey cast iron (samples) having (0.3 wt%) inoculation in thirteen different sections
Hardness
It is observed that hardness and strength increases with wall thickness within the range of 50.3 to 68.5 HRA with decreasing wall thickness from 10 to 2 mm due to refinement of grain structure with thin walls as revealed in Figure 12.
Figure 12:Effect of wall thickness and inoculation on hardness.
The incidence of carbide formation instead of graphite flakes in the resulting microstructure informs the hardness value at 2 and 3 mm. As graphite flakes begin to appear in the microstructure to displace the metastable pearlite and cementite due to rapid solidification, the hardness value begins to decrease steadily also confirmed by Labrecque et al. [13]. The more graphite distribution as the wall thickness increases, the lower the hardness [14]. The incidence of carbide to graphite transition is noticed in the fall in hardness value from 2 to 5 mm.
Tensile Strength
The correlation between tensile strength and wall thickness is shown in Figure 13.
Figure 13:Effect of wall thickness and inoculation against tensile strength.
There is a decrease in the tensile strength with increasing wall thickness. The incidence of the steep fall in tensile strength as the wall thickness increases is an indication of the disappearance of fine carbide microstructure up to 5 mm wall thickness sand gradual emergence and redistribution of graphite flakes which becomes prevalent from 6-10 mm wall thickness.
The regression analysis carried out using the surface fitting of the model. Origin Pro Lab was used to calculate R-Square. The R-Square (Residual Sum of Squares) uses the least square method to minimize the sum of squares of the deviation of the theoretical data points from the experimented data.
The surface fit model obtained for grey iron hardness is given as:
H=−0.0027L6+0.1077L5–1.7385L4+14.21L3−60.791L2+122.73L−22.913 (1)
Where H= the hardness in HRA and L is the wall thickness in mm.
And the surface fit model for the tensile strength is given as:
Ts=−0.0242L6+1.1947L5–22.462L4+204.45L3−921.22L+1756.6L ( 2)
Where Ts=Strength in MPa and L is the thickness in mm.
The surface fit model in equation (i) and (ii) were used to generate theoretical data which was used to obtain the residual. There was a large discrepancy between the experimented data and the predicted values as shown in Tables 4 and 5.
| Wall Thickness | HRA (Exp. Value) | HRA (Pred. Value) |
|---|---|---|
| 2 | 68.5 | 68.5206 |
| 3 | 65.3 | 65.2123 |
| 4 | 58.9 | 58.9606 |
| 5 | 55.4 | 55.0245 |
| 6 | 54.4 | 52.759 |
| 7 | 52.5 | 49.7911 |
| 8 | 52.3 | 44.2518 |
| 9 | 50.6 | 35.0641 |
| 10 | 50.3 | 20.287 |
Table 4: Results of experimental data and model prediction value of the hardness.
| Thickness (mm) | T.S (Exp. Values) | T.S (Pred. Value) |
|---|---|---|
| 2 | 1137 | 1141.21 |
| 3 | 965 | 952.2183 |
| 4 | 731 | 745.6576 |
| 5 | 627 | 625.3125 |
| 6 | 596 | 587.04 |
| 7 | 573 | 583.7251 |
| 8 | 569 | 572.8128 |
| 9 | 537 | 546.4161 |
| 10 | 524 | 544 |
Table 5: Result of experimental data and modal prediction value of the tensile strength
The regression analysis on the two results (hardness and tensile strength) gives Multiple R and Significance of 0.915 and 0.001437 for hardness values and 0.8485 and 0.0077 for tensile strength.
Convergence multivariate regression model
On the basis of the large discrepancies in the experimental data and the predicted values, iteration is performed using the optimized solver analysis. This is done using the relaxation iteration system known as convergence iteration.
When φ is a smooth real-valued function on the real numbers, its second derivative can be approximated by:
Using this in both dimensions for a function φ of two arguments at the point (x, y), and solving for φ (x, y), results in:
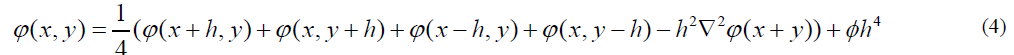
To approximate the solution of the Poisson equation: ε =ϕ∇2 , Numerically on a two-dimensional grid with grid spacing h, the relaxation method assigns the given values of function φ to the grid points near the boundary and arbitrary values to the interior grid points, and then repeatedly performs the assignment:
φ:=φ* on the interior points, where φ* is defined by:
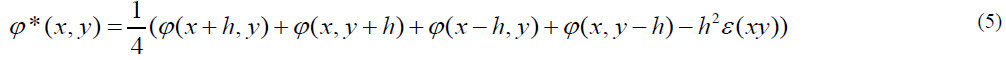
The iteration is used to optimize the coefficient of the independent variable and the sum of square deviation (SSD). The result of the convergence iteration gives the minimum possible value for the coefficients of the independent variable in the model equation for both hardness and tensile function. This is done using the Generalized Reduced Gradient (GRG) non-linear function without any constraints imposed on the variables.
The convergence multivariate regression model equation for hardness (H) as a function of thickness (L) of grey iron cast is now:
H=0.00266665193162911L6+0.107666128403557L5–1.73845369708224L4+14.209534156854L4−60.790463051 8225L2+122.727449735241L−22.913 (6)
And the model equation for tensile strength (Ts) as a function of wall thickness (L) of the grey iron cast is:
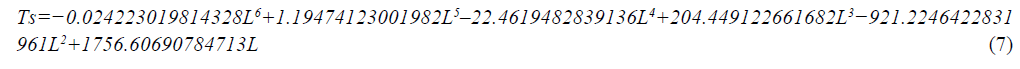
The experimental data and the predicted values using the new model function is given in Tables 6 and 7.
| Wall Thickness (mm) | HRA (Exp. Value) | HRA (Predicted Value |
|---|---|---|
| 2 | 68.5 | 68.51571175 |
| 3 | 65.3 | 65.21673445 |
| 4 | 58.9 | 59.04293887 |
| 5 | 55.4 | 55.41109614 |
| 6 | 54.4 | 54.01491695 |
| 7 | 52.5 | 53.10503469 |
| 8 | 52.3 | 51.84899919 |
| 9 | 50.6 | 50.77128111 |
| 10 | 50.3 | 50.27328693 |
Table 6: Experimental data and Predicted values of Hardness as a function of wall thickness using the optimized (GRG) equation model.
| Wall Thickness (mm) | T.S (Exp. Values) | T.S (Pred. Values) |
|---|---|---|
| 2 | 1137 | 1141.198 |
| 3 | 965 | 952.171 |
| 4 | 731 | 745.516 |
| 5 | 627 | 624.9228 |
| 6 | 596 | 586.0384 |
| 7 | 573 | 581.3539 |
| 8 | 569 | 567.6501 |
| 9 | 537 | 536.0028 |
| 10 | 524 | 524.3478 |
Table 7: Experimental data and predicted values of tensile strength as a function of wall thickness using the optimized (GRG) equation model.
The optimized Multiple R, R-Square and significance F for hardness and tensile strength are 0.9315, 0.8678, 0.000258 and 0.8743, 0.7645, 0.00204, respectively.
The following conclusions are drawn from the research:
Hardness increases with decreased wall thickness due to carbide formation and microstructure refinement. 2 mm thin wall grey iron exhibits fine carbide in ferrite matrix structure due to rapid solidification of the wall. Carbide formation decreases with increased wall thickness with graphite formation and redistribution in ferrite matrix between 6 mm to 10 mm wall thickness. Tensile strength also decreased with increased wall thickness at a steep rate between 2 mm to 5 mm and reduced moderately from 6 mm to 10 mm; the former owing to the rapid disappearing of the fine carbide structure and the later due to the graphite flakes formation and coarse grain redistribution with moderate solidification. Regression analysis on the two results (hardness and tensile strength) gives Multiple R and Significance of 0.915 and 0.001437 for hardness values and 0.8485 and 0.0077 for tensile strength, respectively. The convergence multivariate analytical tool was used to obtain minimum coefficients for the independent variable and adjust the large discrepancies between the experimented data and the predicted values for a robust model equation. The new model equation was generated having 93.15% confidence and 0.02% chance of a random data for hardness. The confidence of 87.4% and 0.2% random chance for tensile strength data which can predict unknown hardness and tensile strength for known wall thickness.
