Review Article - European Journal of Applied Engineering and Scientific Research ( 2018) Volume 6, Issue 1
This paper involves an investigation on the maximal subgroups of the groups of order pqr, a theorem has been stated and prove concerning the nature and behavior of the maximal subgroup of such groups. The group algorithm and programming (GAP) has been applied to enhance and validate the results.
Element, Abelian, Permutation groups
The concept of maximal subgroup is playing a vital role in the application of group series more especially in determining the solvability and nil potency of a group. This research has investigated the maximal subgroups of a permutation group of unique order and carries out research on the behavior of the maximal subgroup.
Definition 1.1
Let G be a group. A subgroup H of G is said to be a maximal subgroup of G if H ≠ G and there is no subgroup K ? G such that H<K<G. Note that a maximal subgroup of G is not maximal among all subgroups of G, but only among all proper subgroups of G. For this reason, maximal subgroups are sometimes called maximal proper subgroups.
Similarly, a normal subgroup N of G is said to be a maximal normal subgroup of G if N ≠ G and there is no normal subgroup K of G, such that N<K<G.
Definition 1.2
A subgroup N of a group G is normal in G if the left and right cossets are the same, that is if gH = Hg ∀g ∈G and a subgroup H of G.
Definition 1.3
The factor group of the normal subgroup N in a group G written as G/N is the set of cosets of N in G.
Definition 1.4
The factor group of the normal subgroup N in a group G written as G/N is the set of cosets of N in G.
Definition 1.5 [1]
A solvable group is a group having a normal series such that each normal factor is abelian.
Definition 1.6 [2]
A group G is nilpotent if it has a normal series G=G0 ≤ G1 ≤ G2 ≤…≤ Gn=(1) where Gi/Gi+1 ≤ Z(G/Gi+1) (centre of G/ Gi+1).
Definition 1.7
A finite group is simple when its only normal subgroups are the trivial subgroup and the whole group.
Definition 1.8 [3]
A group is a p-group if the order is a prime or prime power.
Definition 1.9
Let G be a group, and let p be a prime number. A group of order Pk for some k ≥ 1 is called a p-group.
Theorem 2.1 (Lagrange’s theorem)
Let G be a finite group and H ≤ G. Then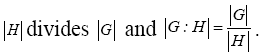 
Proof
Let G be a finite group and let H ≤ G such that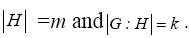 
For any g ? G, define a map Øg:H → gH by Øg (h)=gh. This map is clearly surjective.
Furthermore, for any distinct h1≠h2 ? H, we have that gh1 ≠ gh2. Thus Øg is a bijection,
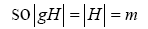
It is easy to see that the set of left cossets of H in G form a partition of G. First note that for any g ? G, g ? gH.
Thus,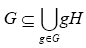 
and clearly 
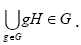Therefore,
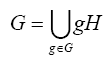
To show that left cossets are disjoint, suppose that for distinct cossets g1H ≠ g2H ? G/H.
There exists an element x ? g1H ∩ g2H. Then there exist elements h1,h2 ? H such that, x=g1h1=g2h2.
Therefore, g1=g2h2h1-1, so for any g1h ? g1H,
g1h=(g2h2h1-1)h= g2(h2h1-1h)? g2H
Hence, g1H ? g2H. But we have seen that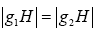 
, so g1H = g2H, which is a contradiction. Thus, the k left cosets of H in G are in fact disjoint and, hence, partition G. Since each has cardinality m, it follows that 
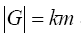. Therefore 
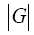divides 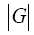and .
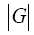Example
If 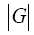=14 then the only possible orders for a subgroup are 1, 2, 7 and 14.
Theorem 2.2 (Cauchy’s theorem for abelian groups)
Let A be a finite abelian group. If p is a prime number that divides its order, then A must have an element of order p.
Theorem 2.3 (Sylow’s first theorem)
Let G be a finite group and p be a prime number such that its power by α is the largest power that will divide 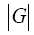Then there exist at least one subgroup of order Pα. Such groups are called Sylow p-subgroups.
Theorem 2.4 (Sylow’s second theorem)
Let np be the number of sylow p-subgroups of a finite group G. Then np≡1 mod.
Theorem 2.5 (Sylow’s third theorem)
Any two Sylow p-subgroups are conjugate.
Theorem 2.6 (Sylow’s fourth theorem)
Any p-subgroup B is contained in a Sylow p-subgroup.
Example
Let G be a group of order 12 [4-6]. Then either G has a normal Sylow 3-subgroup, or else it’s isomorphic to A4.
Reason: 12=22 × 3. We know n3 has to divide 22=4 and it also has to be congruent to 1 mod 3. So it can be either 1 or 4.
If n3=1, then G has a normal Sylow 3-subgroup.
If n3=4, then we know that the four Sylow 3-subgroups are acted on by G, by conjugation. Let’s call the set S={P1,… , P4 } . The action of G gives us a homomorphism Ø : G → S 4 .
We will first show that Ø is injective, then we will show that the image of Ø is A4. This will show that G ≡ imØ = A4 .
To show Ø is injective, we need to show that ker Ø =1.
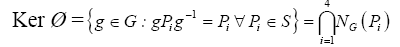
We know that for eachi,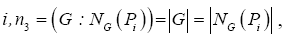 
so we have here that,
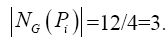Since Pi ≤ NG (Pi) and 
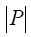is also 3, it means Pi= NG (Pi). So in our case,
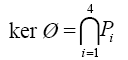
The Pi’s happen, in this case, to be distinct groups of prime order (their order is 3). A general and useful fact about distinct groups of the same prime order is that they can only intersect each other trivially. (Take for example two subgroups P1 and P2 of order p, then the subgroup P1∩P2 has o have order 1 or p. If it has order p then P1=P2, so if P1 and P2 are not the same subgroup P1∩P2 has to have order 1, i.e., it’s the trivial subgroup.)
Applying this to our case we get ker Ø =1. Therefore Ø is injective, and G ≡ imØ
Now G has 4 subgroups, P1,…,P4, of order 3. Each of these subgroups has two elements of order 3 and the identity element.
The two elements of order three have to be different for each Pi (since different Pi ‘s had only the identity element in common).
Therefore G contains 8 different elements of order 3.
Since G is isomorphic to imØ, these 8 different elements of order 3 have to map to 8 different elements of order 3 in S4. The only elements of order three in S4 are 3-cycles. And 3-cycles are even permutations, so are elements in A4.
So A4 ∩ imØ is a subgroup of both A4 and imØ with at least 8 elements. But since both A4 and imØ have 12 elements, this intersection subgroup has to also divide 12. The only factor of 12 that is greater than or equal to 8 is 12. So A4 ∩ imØ is a subgroup of both A4 and imØ of size 12, and since A4 and imØonly have 12 elements anyway, it means A4 ∩ imØ = A4=imØ.
Example
Let G be a group of order 351. Then G has a normal Sylow p-subgroup for some prime p dividing 351.
Reasoning: 351=33 × 13. So a Sylow 3-subgroup would have order 33=27, and a Sylow 13-subgroup would have order 13. Let us start out with what n13 can be n13 divides 27, and
n13=1mod 13. Only two possibilities: n13=1 or 27.
If n13=1, then the Sylow 13-subgroup is a normal subgroup of G, and we are done.
If n13=27, then we are going to show that there can only be room for one Sylow 3-subgroup, and therefore the Sylow 3-subgroup is normal in G. We’ll use the fact that distinct subgroups of order p for some prime p can only have the identity element in their intersection.
(Suppose P1 and P1 are subgroups of order p. Then P1∩ P2 ≤ P1 and P1∩ P2 ≤ P1. So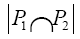 
must be either 1 or p, and the only way it can be p is if P1∩P2 =P1 and P1∩P2 =P2, making P1=P2).
Therefore if P1 and P2 are not the same subgroup, their intersection has order 1, so contains only the identity element. Do be warned, though, that this is only true about subgroups of prime order, so this argument wouldn’t work if, say, the Sylow 13-subgroups had order 132.
Since the Sylow 13-subgroups are subgroups of order 13, they can only intersect each other at the identity element. Also, every element of order 13 forms a subgroup of order 13, which has to be one of the Sylow 13-subgroups. Each Sylow 13 subgroup contains 12 elements of order 13 (every element except for the identity). There are 27 Sylow 13 sub-groups, so there are a total of 27 × 12=324 elements of order 13 in G.
This leaves 351-324=27 elements of G that do not have order 13. Since a Sylow 3-subgroup would have to have exactly 27 elements in it, this means that all these 27 elements form a Sylow 3-subgroup, and it must be the only one (since there are not any extra elements of G to use). So n3=1 and this Sylow 3-subgroup must be normal in G.
Proposition 2.7 [5]
A group G is a direct product of subgroups H1,H2 if and only if
a) G=H1H2
b) H1 ∩ H2={e} and
c) Every element of H1 commutes with every element of H2
Proof
If G is the direct product of H1 and H2, then certainly (a) and (c) hold and (b) holds because, for any g ? H1∩H2, the element (g, g-1) maps to e under (H1,H2)→H1H2 and so equals to (e,e).
Conversely, (c) implies that (H1,H2)→H1H2 is a homomorphism and (b) implies that it is injective:
H1H2=e →H1=H2-1 ? H1 ∩ H2={e}. Finally, (a) implies that it is surjective.
A group G is a direct product of subgroups H1,H2 if and only if
a) G=H1,H2
b) H1∩ H2={e}
c) H1 and H2 are both normal in G
Proof
Certainly, these conditions are implied by those in proposition 1.37 and so it remains to show that they imply that each element H1 of H1 commutes with each element H2 of H2. Two elements H1 and H2 of G commute if and only if their commutator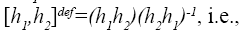 
e but
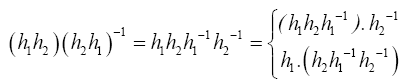
Which is in h2 because h2 is normal and is in H1 because H1 is normal. Therefore (b) implies that [H1,h2]=e.
Proposition 2.9 [9]
(i) Subgroups H ⊂ G and quotient groups G/K of a solvable group G are solvable.
If normal subgroup N ? G is solvable and if the quotient G/N is solvable then G is solvable.
Proof
H(n) ⊂ G(n) for all n. Also G(n) maps onto (G/N)(n) for all n.
If (G/N)(n) ={1} then G(n) ⊂ N. So if N(m)={1} then G(N+M) ⊂ N(M)={1}
Corollary 2.10 [8]
All p-groups are solvable.
Proof
Let P be a p-group. We will induct on n, where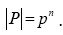 
If 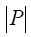= p, then P is cyclic. Therefore, P is abelian and, hence, solvable. Suppose that for all 1 ≤ k < n, groups of order Pk are solvable.
Let 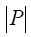= pn By Corollary 1, Z. (P) ≠ 1 Thus, P / Z (P) = pk (for some k<n). So, by the inductive hypothesis, P=Z(P) is solvable. Since Z P is abelian, then Z(P) is solvable. Thus, by Proposition 1, P is solvable. Therefore, by induction, all p-groups are solvable.
Theorem 2.11 [9]
A finite group is nilpotent if and only if it is a direct product of its Sylow subgroups.
Proof
Finite p-groups are nilpotent by theorem 1.4 and hence so are any direct product of p-groups.
Now suppose that G is a finite nilpotent group and let P be any Sylow subgroup of G. Let N=NG (P). Suppose N<G. Then by Corollary 1 N<NG (N).
Let x ? NG (N)-N Hence x-1Px ≤ x-1NX=N and so x-1Px is a Sylow subgroup of N as is P. It follows that y-1x-1Pxy=P for some y ? N and so xy ? N.
But y∈ N and x∉ N a contradiction. It must therefore be that N=G and so P is normal in G. G is therefore the direct product of its Sylow subgroups.
Theorem 2.12 [3]
Finite p-groups are nilpotent.
Proof
Zr+1(G)/Zr(G)=Z(G/Zr(G)). Since the centre of a non-trivial p-group is non-trivial Zr (G)<Zr+1 (G) unless Zr (G)=G .
Proposition 2.13 [3]
Every nilpotent group is solvable.
Proof
If G is nilpotent group then the upper central series of G.
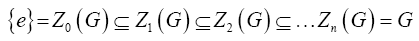is a normal series.
Moreover for every i we have,
Zi(G)/Zi-1=Z(G/Zi-1(G))
So all quotients of the upper central series are abelian.
Theorem 2.14
A normal subgroup N of a group G is a maximal normal subgroup if and only if the quotient G/N is simple.
Theorem 2.15
Let G be a group of order pqr where p=r and p,q,r distinct primes. The maximal subgroups of G are of order qr and pqr-1 which are solvable.
Proof
Suppose G is a group of order pqr. By theorem 2.1, the possibility for the order of subgroups of G are p, pq, pq2, …, pqr-1, pqr, q, q2,…, qr-1, qr. It is clear that pqr-1 and qr are the maximal subgroups of G since they are not contained in any other proper subgroups of G.
It remains to show that the two maximal subgroups are solvable and nilpotent. qr is solvable by Corollary 2.10.
What left is to show that pqr-1 is solvable. Let G1 be a group of order pqr-1, the sylow p and q subgroups of G1 are normal in the group. Let H1 be the Sylow p-subgroup of G1 then,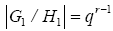 
. Since q is prime then G1/H1 and H1 are solvable by corollary 2.10, it follows that G1 is solvable by (ii) of proposition 2.
Consider the permutation groups C1 and D1
C1={(1),(123),(132)},D1={(1),(46)} acting on the sets S1={123} and Δ1={46}, respectively.
Let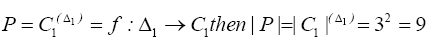 
We can easily verify that G1 is a group with respect to the operations
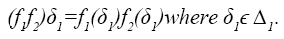
The wreath products of C1 and D1 is given by W1 as it appears in the result validation which is given by the (GAP) below:
gap>C1:=Group ((1, 2, 3));
Group ([(1, 2, 3)])
gap>D1:=Group ((4, 6));
Group ([(4, 6)])
gap>W1:=Wreath Product (C1, D1);
Group ([(1, 2, 3), (4, 5, 6), (1, 4) (2, 5) (3, 6)])
gap>Maximal Subgroup Class Reps (W1);
[Group ([ (1, 3, 2) (4, 6, 5) (1, 2, 3) (4, 6, 5)]), Group ([(1, 4) (2, 5) (3, 6), (1, 2, 3) (4, 6, 5)]), Group ([(1, 4) (2, 5) (3, 6), (1, 3, 2) (4, 6, 5)])]
gap>M1:=Group ([(1, 3, 2) (4, 6, 5) (1, 2, 3) (4, 6, 5)]);
Group([(1, 3, 2) (4, 6, 5) (1, 2, 3) (4, 6, 5)])
gap>Is Solvable (M1);
true
gap>Is Nilpotent (M1);
true
gap>Is Normal (W1, M1);
true
gap>Is Simple (M1);
false
gap>Is Transitive (M1);
false
gap>Is Primitive (M1);
false
gap>M2:=Group ([(1, 4) (2, 5) (3, 6) (1, 2, 3) (4, 6, 5)]);
Group ([(1, 4) (2, 5) (3, 6) (1, 2, 3) (4, 6, 5)])
gap>Is Solvable (M2);
true
gap>Is Nilpotent (M2);
false
gap>Is Normal (W1, M2);
true
gap>Is Simple (M2);
false
gap>Is Transitive (M2);
true
gap>Is Primitive (M2);
false
gap>M3:=Group ([(1, 4) (2, 5) (3, 6) (1, 3, 2) (4, 6, 5)]);
Group ([(1, 4) (2, 5) (3, 6) (1, 3, 2) (4, 6, 5)])
gap>Is Solvable (M3);
true
gap>Is Nilpotent (M3);
true
gap>Is Normal (W1, M3);
false
gap>Is Simple (M3);
false
gap>Is Transitive (M3);
true
gap>Is Primitive (M3);
false
gap>quit;
Consider the permutation groups C2and D2
C2={(1), (15432), (14253), (13524), (12345)}
D2={(1), (678), (687)} acting on the sets S2 ={1, 2, 3, 4, 5} and Δ2 ={6, 7, 8}, respectively.
Let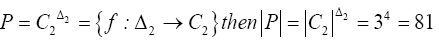 
We can easily verify that G1 is a group with respect to the operations
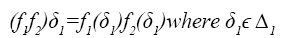
The wreath products of C2 and D2 is given by W1 as it appears in the result validation which is given by the (GAP) below:
gap>C2:=Group ((1, 2, 3, 4, 5));
Group ([(1, 2, 3, 4, 5)])
gap>D2:=Group ((6, 7, 8));
Group ([(6, 7, 8)])
gap>W2:=Wreath Product (C2, D2);
Group ([(1, 2, 3, 4, 5) (6, 7, 8, 9, 10) (11, 12, 13, 14, 15) (1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15)])
gap>Maximal Subgroup Class Reps (W2);
[Group ([(1, 3, 5, 2, 4) (6, 8, 10, 7, 9) (11, 13, 15, 12, 14) (1, 2, 3, 4, 5) (11, 15, 14, 13, 12) (1, 5, 4, 3, 2) (6, 7, 8, 9, 10)])
Group ([ (1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15) (1, 2, 3, 4, 5) (11, 15, 14, 13, 12) (1, 5, 4, 3, 2) (6, 7, 8, 9, 10)])
Group ([(1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15) (1, 3, 5, 2, 4) (6, 8, 10, 7, 9) (11, 13, 15, 12, 14)])]
gap>M4:=Group ([(1, 3, 5, 2, 4) (6, 8, 10, 7, 9) (11, 13, 15, 12, 14) (1, 2, 3, 4, 5) (11, 15, 14, 13, 12) (1, 5, 4, 3, 2) (6, 7, 8, 9, 10)]);
Group ([(1, 3, 5, 2, 4) (6, 8, 10, 7, 9) (11, 13, 15, 12, 14) (1, 2, 3, 4, 5) (11, 15, 14, 13, 12) (1, 5, 4, 3, 2) (6, 7, 8, 9, 10)]) gap>Is Solvable (M4);
true
gap>Is Nilpotent (M4);
true
gap>Is Normal (W2, M4);
true
gap>Is Simple (M4);
false
gap>Is Transitive (M4);
false
gap>Is Primitive (M4);
false
gap>M5:=Group ([(1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15) (1, 2, 3, 4, 5) (11, 15, 14, 13, 12) (1, 5, 4, 3, 2) (6, 7, 8, 9, 10)]);
Group ([(1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15) (1, 2, 3, 4, 5) (11, 15, 14, 13, 12) (1, 5, 4, 3, 2) (6, 7, 8, 9, 10)])
gap>Is Solvable (M5);
true
gap>Is Nilpotent (M5);
false
gap>Is Normal (W2, M5);
true
gap>Is Simple (M5);
false
gap>Is Transitive (M5);
true
gap>Is Primitive (M5);
false
gap>M6:=Group ([(1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15) (1, 3, 5, 2, 4) (6, 8, 10, 7, 9) (11, 13, 15, 12, 14)]);
Group ([(1, 6, 11) (2, 7, 12) (3, 8, 13) (4, 9, 14) (5, 10, 15) (1, 3, 5, 2, 4) (6, 8, 10, 7, 9) (11, 13, 15, 12, 14)])
gap>Is Solvable (M6);
true
gap>Is Nilpotent (M6);
false
gap>Is Normal (W2, M6);
true
gap>Is Simple (M6);
false
gap>Is Transitive (M6);
true
gap>Is Primitive (M6);
false
gap>quit;
Consider the permutation groups C3 and D3
C3={(1), (15432), (14253), (13524), (12345)}
D3={(1), (678), (687)} acting on the sets S3 ={1, 2, 3, 4, 5} and Δ3 ={6, 7, 8}, respectively.
Let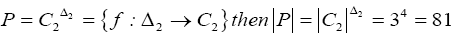 
We can easily verify that G1 is a group with respect to the operations
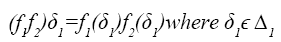
The wreath products of C3 and D3 is given by W3 as it appears in the result validation which is given by the (GAP) below:
gap>C3:=Group ((1, 2, 3));
Group ([(1, 2, 3)])
gap>D3:=Group ((4, 5, 6, 7, 8));
Group ([ (4, 5, 6, 7, 8)])
gap>W3:=Wreath Product (C3, D3);
Group ([(1, 2, 3) (4, 5, 6) (7, 8, 9) (10, 11, 12) (13, 14, 15) (1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15)])
gap>Maximal Subgroup Class Reps (W3);
[Group ([ (1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6) ])
Group ([(1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)])
Group ([(1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14)])]
gap>M7:=Group ([(1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)]);
Group ([(1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)])
gap>Is Solvable (M7);
true
gap>Is Nilpotent (M7);
false
gap>Is Normal (W3, M7);
true
gap>Is Simple (M7);
false
gap>Is Transitive (M7);
true
gap>Is Primitive (M7);
false
gap>M8:=Group ([(1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)]);
Group ([(1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)])
gap>Is Solvable (M8);
true
gap>Is Nilpotent (M8);
true
gap>Is Normal (W3, M8);
true
gap>Is Simple (M8);
false
gap>Is Transitive (M8);
false
gap>Is Primitive (M8);
false
gap>Maximal Subgroup Class Reps (W3);
[Group ([ (1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)])
Group ([(1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14) (1, 2, 3) (13, 15, 14) (1, 2, 3) (10, 12, 11) (1, 2, 3) (7, 9, 8) (1, 3, 2) (4, 5, 6)])
Group ([(1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14)])]
gap>M9:=Group ([(1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14)]);
Group ([(1, 4, 7, 10, 13) (2, 5, 8, 11, 14) (3, 6, 9, 12, 15) (1, 3, 2) (4, 6, 5) (7, 9, 8) (10, 12, 11) (13, 15, 14)])
gap>Is Solvable (M9);
true
gap>Is Nilpotent (M9);
true
gap>Is Normal (W3, M9);
false
gap>Is Simple (M9);
false
gap>Is Transitive (M9);
true
gap>Is Primitive (M9);
false
gap>
My acknowledgements go the Allah that gives me the knowledge and the opportunity to write this paper. I also want to acknowledge Federal University Kashere for funding this research.
